Icosahedral grid-based density estimation

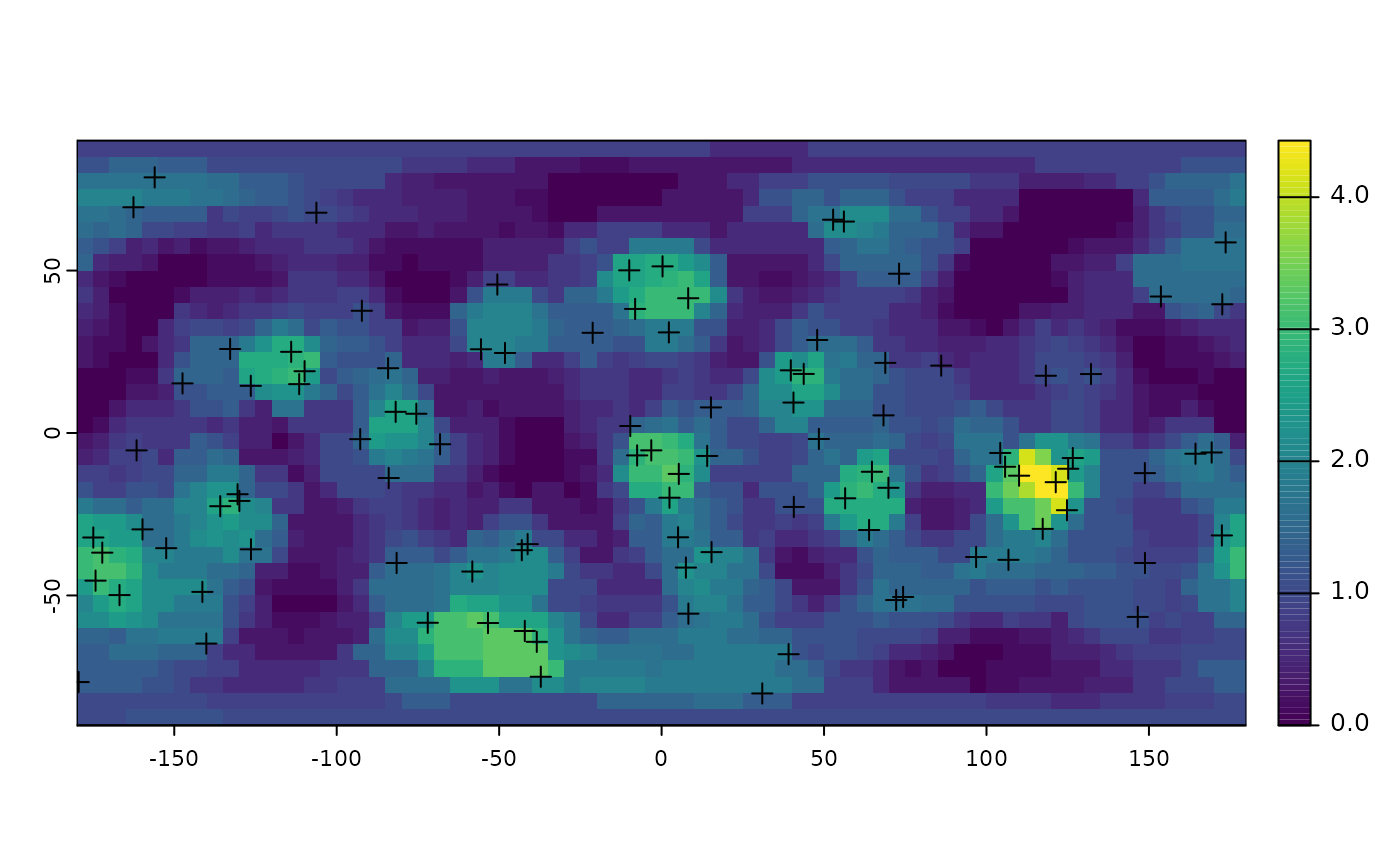
Spatial density estimation algorithm based on rotation of icosahedral grids.

Usage

gridensity(x, y, out, trials = 100, FUN = mean)

Arguments

x

Matrix of longitude, latitude data, sf class, or SpatialPoints Point cloud.

y

trigrid or hexagrid An icosahedral grid.

out

trigrid, hexagrid or SpatRasteroutput structure.

trials

numeric value, the number of iterations.

FUN

function The function to be applied on the iteration results.

Value

Either named numeric vector, or a SpatRaster object. If FUN is set to NULL, the output will be either a matrix or SpatRaster.

Details

Any points set can be binned to an icosahedral grid (i.e. number of incidences can be counted), which will be dependent on the exact positions of grid cells. Rotating the grid in 3d space will result in a different distribution of counts. This distribution can be resampled to a standard orientation structure. The size of the icosahedral grid cells act as a bandwidth parameter.

The implemented algorithm 1) takes a point cloud (x)) and an icosahedral grid y 2) randomly rotates the icosahedral grid, 3) looks up the points falling on grid cells, 4) resamples the grid to a constant orientation object (either trigrid, hexagrid or SpatRaster). Steps 2-4 are repeated trial times, and then FUN is applied to every vector of values that have same spatial position.

Examples

# example to be run if terra is present
if(requireNamespace("terra", quietly=TRUE)){

 # randomly generated points
 x <- rpsphere(100, output="polar")

 # bandwidth grid
 y <- hexagrid(deg=13)

 # output structure
 out <- terra::rast(res=5)

 # the function
 o <- gridensity(x, y, out, trials=7)

 # visualize results
 terra::plot(o)
 points(x, pch=3)
}
#> Selecting hexagrid with tessellation vector: c(3).
#> Mean edge length: 13.35 degrees.
#> 1 
2 
3 
4 
5 
6 
7